Descobrindo padrões ocultos através da aprendizagem por máquina: lições do FizzBuzz para o Apache MXNet.

Quando o cientista de dados Joel Grus escreveu um artigo sobre o uso da máquina para resolver o problema “fizzbuzz” no ano passado, a maioria das pessoas o via como um exercício de comédia, talvez com um aviso sobre o uso inadequado de AI. Mas vimos uma lição mais profunda. Certamente, você não precisa de AI para resolver fizzbuzz, desde que alguém lhe diga o algoritmo subjacente ao problema. Mas suponha que você descubra um padrão aparentemente aleatório como a produção de fizzbuzz na natureza? Padrões como esse existem ao longo da vida real, e ninguém nos dá o algoritmo. O aprendizado da máquina resolve tais problemas.
Este verão, tive a oportunidade de entrevistar com uma inicialização de AI que eu realmente gostei. E adivinha? Me pediram para resolver fizzbuzz usando aprendizagem profunda. Longa história, não recebi a oferta de emprego.
Mas isso nos fez pensar sobre porque o fizzbuzz faz sentido como uma aplicação de aprendizagem profunda. Na superfície, é um problema tolo na aritmética inteira (ou teoria dos números, se você gosta de ser pedante). Mas gera padrões interessantes, e se você viu uma lista de entradas e saídas sem saber o algoritmo subjacente, encontrar uma maneira de prever as saídas seria difícil. Portanto, fizzbuzz é uma maneira fácil de gerar padrões nos quais você pode testar técnicas de aprendizado profundo. Neste artigo, tentaremos as ferramentas populares do Apache MXNet e descobriremos que esse pequeno exercício leva mais esforço do que se poderia esperar.
O que é fizzbuzz?
De acordo com a Wikipedia , o fizzbuzz se originou como jogo infantil, mas há muito tempo tem sido um desafio popular que os entrevistadores dão aos candidatos de programação. Dado um número inteiro x , o programador deve produzir saída de acordo com as seguintes regras:
- se
xfor divisível por 3, a saída é “fizz” - se
xfor divisível em 5, a saída é “buzz” - se
xfor divisível por 15, a saída é “fizzbuzz” - senão, a saída é
x
Uma sequência de saída típica será assim:
| Entrada | Saída |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | “fizz” |
| 4 | 4 |
| 5 | “zumbido” |
| 6 | “fizz” |
| 7 | 7 |
| 8 | 8 |
| 9 | “fizz” |
| 10 | “zumbido” |
| 11 | 11 |
| 12 | “fizz” |
| 13 | 13 |
| 14 | 14 |
| 15 | “fizzbuzz” |
| 16 | 16 |
Os requisitos geram uma máquina de estado surpreendentemente complexa, para que eles possam revelar se um candidato a programação iniciante tem boas habilidades organizacionais. Mas se conhecemos as regras que geram os dados, realmente não há necessidade de aprendizado automático. Infelizmente, na vida real, nós só temos os dados. O aprendizado automático da máquina nos ajuda a criar um modelo de dados. Neste aspecto, a fizzbuzz nos fornece um conjunto de dados fácil de entender e nos permite compreender e explorar os algoritmos.
O que se segue é um exercício pedante para entender como o MXNet pode ser usado para resolver o problema do fizzbuzz.
O que é o MXNet?
O MXNet é um framework de aprendizado profundo escalável de código aberto com uma ampla base de suporte . É suportado por Amazon, Intel, Dato, Baidu, Microsoft e MIT, entre outros.
MXNet oferece as seguintes vantagens :
- Posicionamento do dispositivo: é fácil especificar onde cada estrutura de dados deve viver (CPU versus GPU).
- Treinamento multi-GPU: é fácil escalar os cálculos com mais GPUs.
- Diferenciação automática: automatiza os cálculos de derivadas.
- Camadas predefinidas otimizadas: as camadas pré-definidas são otimizadas para velocidade.
Nós usamos isso neste artigo por causa de sua popularidade e porque é uma das estruturas mais flexíveis no aprendizado profundo.
Estrutura do artigo
Nas seções subsequentes, faremos o seguinte:
- Estrutura o problema como um problema de classificação multi-classe
- Gerar os dados do fizzbuzz
- Divida os dados no trem e teste
- Criar um modelo de regressão logística no MXNet a partir do zero
- Introduzir
gluon - Construa um modelo de percepção multicamada usando
gluon
Os exemplos são codificados em Python porque é compacto e conhecido.
Estrutura o problema
Dado os dados, como estruturamos isso como um problema de aprendizado de máquina? Para realizar a aprendizagem de máquinas supervisionada, precisamos de recursos e uma variável de destino. O fizzbuzz pode ser modelado como um problema de classificação multi-classe.
-
Entrada: pensemos em uma maneira de fazer engenharia de recursos para a entrada. A entrada é um número inteiro. Uma opção, que Joel Grus empregou em seu artigo, é converter o número em sua representação binária. A representação binária pode ser de comprimento fixo, e cada dígito da representação binária de comprimento fixo pode ser uma característica de entrada.
-
Alvo: o alvo pode ser uma das quatro classes – fizz , buzz , fizzbuzz ou o número dado . O modelo deve prever qual das classes é mais provável para um número de entrada. Depois que as quatro classes são codificadas e o modelo é construído, retornará um dos quatro rótulos de predição. Então, também precisaremos de uma função decodificador para converter a etiqueta na saída correspondente.
Um exemplo explicará isso melhor.
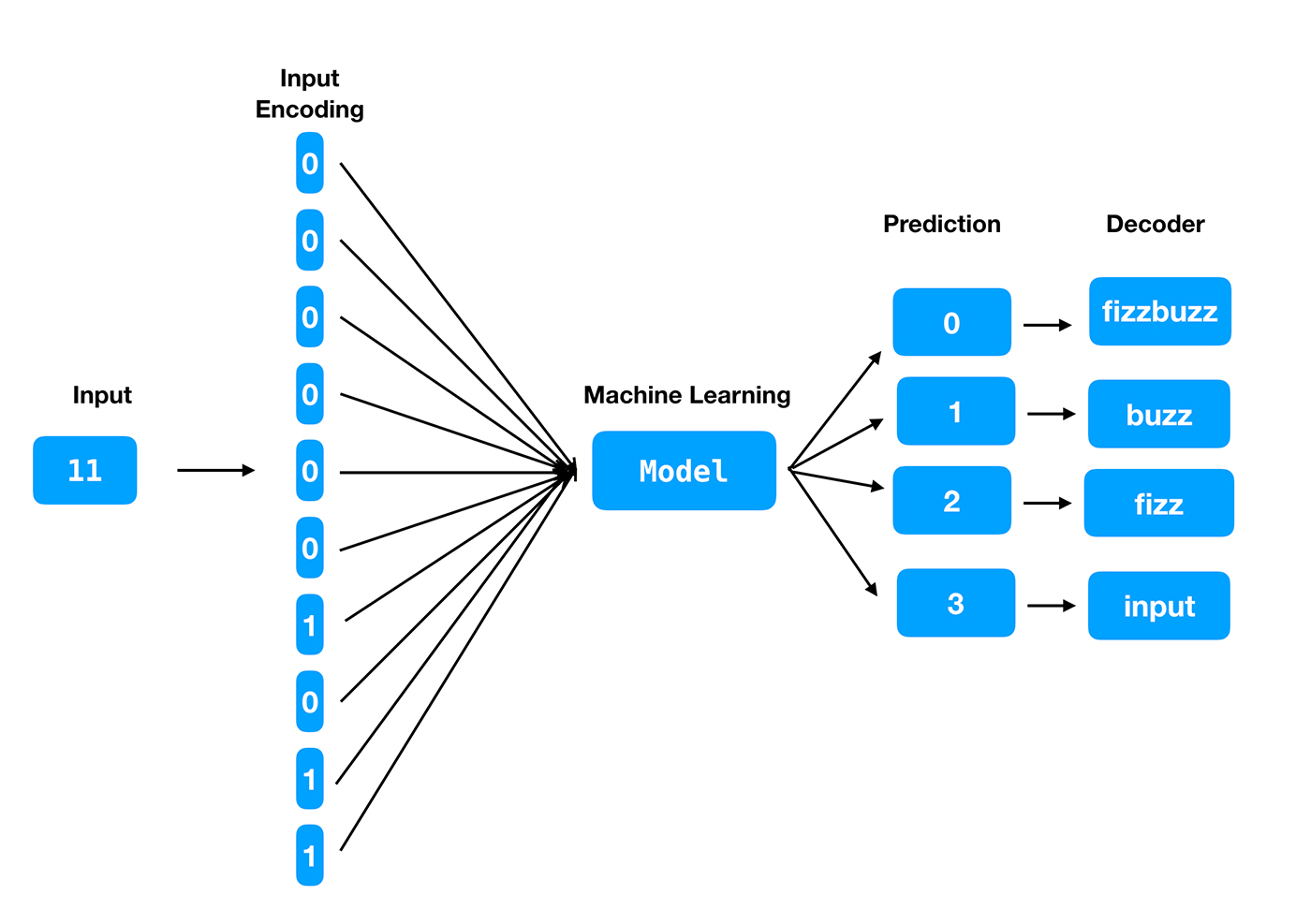
Digamos que treinamos o modelo usando os primeiros 1.000 inteiros. Para criar uma representação binária de comprimento fixo, primeiro precisamos encontrar o comprimento máximo do vetor de entrada. Todos os números até 1000 podem ser representados em binário dentro do tamanho 2 10 (que é 1.024), então, precisamos que o vetor de entrada seja do comprimento 10.
A saída é codificada nas etiquetas de predição como 0, 1, 2, 3 para “fizzbuzz”, “buzz”, “fizz” e “o número dado”, respectivamente.
Exemplo
Entrada: 11 (o número dado)
Saída: 11

Cada dígito do vetor de característica de entrada será um neurônio de entrada. A saída terá quatro neurônios, um correspondente a cada um dos rótulos.
A Figura 2 descreve esse processo.
Agora vamos começar a construir modelos usando o MXNet.
Instalando e configurando o MXNet
Para obter o software que precisamos para este exemplo, vamos primeiro importar as bibliotecas Python necessárias numpy e mxnet .
Uma maneira de instalar o mxnet é executar o seguinte comando “
#install mxnet. If its already available, upgrade it.!pipinstallmxnet--upgrade--pre
#import librariesimportnumpyasnpimportmxnetasmximportosmx.random.seed(1)
No mxnet , cada matriz tem um contexto, seja em uma GPU ou CPU.
O tamanho dos dados não será muito alto para este exercício, e uma única CPU deve ser suficiente.
#Define the context to be CPUctx=mx.cpu()
Funções auxiliares
Precisamos de algumas funções auxiliares para começar.
Primeiro, uma função para converter o darn inteiro de entrada em sua forma binária.
#function to encode the integer to its binary representationdefbinary_encode(i,num_digits):returnnp.array([i>>d&1fordinrange(num_digits)])
Em seguida, uma função para codificar o alvo em uma das quatro classes.
#function to encode the target into multi-classdeffizz_buzz_encode(i):ifi%15==0:return0elifi%5==0:return1elifi%3==0:return2else:return3
Uma vez que o modelo é construído e o usamos para prever o rótulo de predição para um determinado número, precisamos de uma função decodificador: uma função que mapeia a previsão para a saída certa. A seguinte função nos ajuda a fazer isso:
#Given prediction, map it to the correct output labeldeffizz_buzz(i,prediction):ifprediction==0:return"fizzbuzz"elifprediction==1:return"buzz"elifprediction==2:return"fizz"else:returnstr(i)
Criando trem, validação, conjuntos de dados de teste
Agora precisamos criar conjuntos de dados de trem, validação e teste.
Vamos gerar 100.000 pontos de dados, representando os inteiros de 1 a 100.000.
No caso ideal, os conjuntos de dados de trem, validação e teste são selecionados aleatoriamente. Mas, por uma questão de simplicidade, vamos usar os primeiros 100 inteiros como conjunto de dados de teste. (Porque sabemos como o fizzbuzz funciona, sabemos que os valores de saída são distribuídos de forma bastante uniforme em todos os números inteiros, portanto, não precisamos nos preocupar com a amostra de dados de teste. Mas lembre-se de que em uma configuração da vida real, os dados de entrada O conjunto é arrastado e os conjuntos de dados de treinamento, validação e teste são escolhidos aleatoriamente.) Uma vez que criamos o modelo, verificamos a precisão do modelo ao prever o conjunto de dados de teste.
Usaremos os inteiros de 101 a 50.000 – essencialmente a metade inferior da faixa de dados – como o conjunto de dados de treinamento. Vamos construir o modelo usando este conjunto de dados.
Usaremos números inteiros de 50,001 a 100,000 – a metade superior do intervalo de dados – como conjunto de dados de validação. Poderíamos usar isso para o ajuste de hiper parâmetros, mas neste exercício, não estaremos fazendo sintonias com hiper parâmetros.
Começamos definindo o número de inteiros a gerar:
#Number of integers to generateMAX_NUMBER=100000
Esse número também determina o comprimento do vetor de características de entrada. Determinamos o número de bits necessários para a representação binária, adicionando 1 porque rodamos o logaritmo para o próximo inteiro inferior.
#The input feature vector is determined by NUM_DIGITSNUM_DIGITS=np.log2(MAX_NUMBER).astype(np.int)1
Os conjuntos de dados de trem, teste e validação são gerados.
#Generate training dataset - both features and labelstrainX=np.array([binary_encode(i,NUM_DIGITS)foriinrange(101,np.int(MAX_NUMBER/2))])trainY=np.array([fizz_buzz_encode(i)foriinrange(101,np.int(MAX_NUMBER/2))])
#Generate validation dataset - both features and labelsvalX=np.array([binary_encode(i,NUM_DIGITS)foriinrange(np.int(MAX_NUMBER/2),MAX_NUMBER)])valY=np.array([fizz_buzz_encode(i)foriinrange(np.int(MAX_NUMBER/2),MAX_NUMBER)])
#Generate test dataset - both features and labelstestX=np.array([binary_encode(i,NUM_DIGITS)foriinrange(1,101)])testY=np. array ([ fizz_buzz_encode ( i ) for i in range ( 1 , 101 )])
Agora que criamos os conjuntos de dados de trem, teste e validação, vamos carregá-los em instâncias de mxnet do iterador do NDArrayIter . Ele nos permite especificar o tamanho do lote para o treinamento e para definir um sinalizador para alejar os dados ou não.
#Define the parametersbatch_size=100num_inputs=NUM_DIGITSnum_outputs=4
#Create iterator for train, test and validation datasetstrain_data=mx.io.NDArrayIter(trainX,trainY,batch_size,shuffle=True)val_data=mx.io.NDArrayIter(valX,valY,batch_size,shuffle=True)test_data=mx.io.NDArrayIter(testX,testY,batch_size,shuffle=False)
Precisamos escrever outra função auxiliar para avaliar a precisão do modelo. Depois que as previsões são geradas, esta função usa métodos MXNet para retornar um número de ponto flutuante de 0 a 1 que indica o quão bem a função se mantém contra o conjunto de dados de validação.
#Function to evaluate accuracy of the modeldefevaluate_accuracy(data_iterator,net):acc=mx.metric.Accuracy()data_iterator.reset()fori,batchinenumerate(data_iterator):data=batch.data[0].as_in_context(ctx)label=batch.label[0].as_in_context(ctx)output=net(data)predictions=n "> nd.argmax(output,axis=1)acc.update(preds=predictions,labels=label)returnpredictions,acc.get()[1]
Regressão logística a partir do zero
Nós temos os dados e as funções auxiliares no lugar.
Para entender uma rede neural simples, vamos construir um modelo de regressão logística de várias classes a partir do zero usando o MXNet. Para construir a partir do zero, é isso que precisamos fazer:
- Inicialize pesos e tendências para valores aleatórios
- Calcule o passe para a frente
- Para cada observação, os recursos e pesos de entrada são multiplicados, adicionados com viés e passados para a função sigmoid. Essa é a saída prevista para essa entrada.
- Calcule o erro
- Atualize os pesos e a polarização usando a descida gradiente
- Repita as etapas 2-4 até a convergência ou para um número específico de épocas
Este artigo faz um trabalho maravilhoso de criar uma regressão logística de várias classes a partir do zero usando o MXNet.
Além disso, o mxnet vem com um pacote de autograd , que permite a diferenciação automática das operações do NDArray e é usado para calcular os gradientes da função de perda em relação aos pesos do modelo.
#import autograd packagefrommxnetimportautograd,nd
O primeiro passo de programação é inicializar a viatura e a matriz de peso.
#Initialize the weight and bias matrix#weights matrixW=nd.random_normal(shape=(num_inputs,num_outputs))#bias matrixb=nd.random_normal(shape=num_outputs)#Model parametersparams=[W,b]
O próximo passo é anexar o autograd para calcular os gradientes de cada parâmetro.
forparaminparams:param.attach_grad()
Queremos que a saída seja a probabilidade para cada uma das classes. A soma das probabilidades deve somar uma, que podemos obter executando a seguinte função softmax.
defsoftmax(y_linear):exp=nd.exp(y_linear-nd.max(y_linear))norms=nd.sum(exp,axis=0,exclude=True).reshape((-1,1))returnexp/norms
A função de perda que usaremos é a entropia cruzada de softmax. A entropada cruzada maximiza a probabilidade de logar com os rótulos corretos. Mais informações sobre a entropia cruzada de softmax podem ser lidas aqui .
#loss functiondefsoftmax_cross_entropy(yhat,y):return-nd.nansum(y*nd.log(yhat),axis=0,exclude=True)
Agora definimos o modelo.
defnet(X):y_linear=nd.dot(X,W)byhat=softmax(y_linear)returnyhat
Para que o modelo aprenda (atualize) os parâmetros do modelo (pesos e preconceitos), precisamos definir um otimizador. A descida gradiente estocástica é um dos métodos mais populares para atualizar os parâmetros.
#Define the optimizerdefSGD(params,lr):forparaminparams:param[:]=param-lr*param.grad
Permite executar os laços de treinamento. Para cada etapa de treinamento, batch_size determina o número de pontos de dados que serão passados pela rede para que ele aprenda. Uma vez que todos os pontos de dados são passados através da rede, uma época é concluída. As épocas de parâmetros definem o número de vezes que o conjunto de dados inteiro deve ser alternado através do processo de treinamento. Escolheremos um número bastante grande de épocas, por isso damos ao framework uma boa chance de aprender o padrão.
#hyper parameters for the trainingepochs=100learning_rate=.01smoothing_constant=.01
Vamos agora executar a função de treinamento.
foreinrange(epochs):#at the start of each epoch, the train data iterator is resettrain_data.resetcódigo>()fori,batchinenumerate(train_data):data=batch.data[0].as_in_context(ctx)label=batch.label[0].as_in_context(ctx)label_one_hot=nd.one_hot(label,4)withautograd.record():output=net(data)loss=softmax_cross_entropy(output,label_one_hot)loss.backward()SGD(params,learning_rate)curr_loss=nd.mean(loss).asscalar()moving_loss=(curr_lossif((i==0)and(e==0))else(1-smoothing_constant)*moving_loss(smoothing_constant)*curr_loss)#the training and validation accuracies are computed_,val_accuracy=evaluate_accuracy(val_data,net)_,train_accuracy=evaluate_accuracy(train_data,net)("Epoch%s. Loss:%s, Train_acc%s, Val_acc%s"%(e,moving_loss,train_accuracy,val_accuracy))
Epoch 99. Loss: 1.18811465231, Train_acc 0.532825651303, Val_acc 0.5332
Durante 100 épocas, a precisão do trecho e a precisão de validação não parecem excelentes. É apenas cerca de 53%. Vamos verificar a precisão no conjunto de dados de teste.
#model accuracy on the test datasetpredictions>, test_accuracy = evaluate_accuracy ( test_data , net ) output = np . vectorize
( fizz_buzz )( np . arange ( 1 , 101 ), predictions . asnumpy () . astype ( np . int )) print
( output ) print ( "Test Accuracy : " , test_accuracy )
['1' '2' '3' '4' '5' '6' '7' '8' '9' '10' '11' '12' '13' '14' '15' '16' '17' '18' '19' '20' '21' '22' '23' '24' '25' '26' '27' '28' '29' '30' '31' '32' '33' '34' '35' '36' '37' '38' '39' '40' '41' '42' '43' '44' '45' '46' '47' '48' '49' '50' '51' '52' '53' '54' '55' '56' '57' '58' '59' '60' '61' '62' '63' '64' '65' '66' '67' '68' '69' '70' '71' '72' '73' '74' '75' '76' '77' '78' '79' '80' '81' '82' '83' '84' '85' '86' '87' '88' '89' '90' '91' '92' '93' '94' '95' '96' '97' '98' '99' '100'] Test Accuracy : 0.53
A precisão no conjunto de dados de teste também é de 53%. O modelo não parece estar funcionando bem.
O que é gluon ?
A biblioteca gluon no Apache MXNet fornece uma API clara, concisa e simples para aprendizagem profunda. Gluon facilita o protótipo, a construção e a formação de modelos de aprendizado profundo sem sacrificar a velocidade de treino.
Gluon suporta programação tanto imperativa como simbólica, facilitando a formação de modelos complexos de forma imperativa. Mais detalhes podem ser encontrados aqui .
Perceptron de várias camadas usando gluon
Vamos construir um modelo de perceptron de várias camadas (MLP) usando gluon .
O MLP é um dos modelos de aprendizagem mais simples. Ele executa dados através de várias camadas, usando comentários para refinar as camadas de processamento (veja a Figura 3). Mais detalhes podem ser encontrados na Wikipédia .

Primeiro precisamos importar gluon :
#import gluonfrommxnetimportgluon
#reset the training, test and validation iteratorstrain_data.reset()val_data.reset()test_data.reset()
Agora, defina o modelo sequencial gluon. Cada camada oculta é adicionada sequencialmente. A variável num_hidden define o número de neurônios em cada uma das camadas ocultas. A função de ativação relu é usada em cada uma das camadas.
#Define number of neurons in each hidden layernum_hidden=64#Define the sequential networknet=gluon.nn.Sequential()withs = "n"> net.name_scope():net.add(gluon.nn.Dense(num_inputs,activation="relu"))net.add(gluon.nn.Dense(num_hidden,activation="relu"))net.add(gluon.nn.Dense(num_hidden,activation="relu"))net.add(gluon.nn.Dense(num_outputs))
Semelhante ao exercício anterior, onde construímos o modelo a partir do zero, os parâmetros precisam ser inicializados.
#initialize parametersnet.collect_params().initialize(mx.init.Xavier(magnitude=2.24),ctx=ctx)
A função de perda é definida, como no exemplo anterior, como entropia cruzada de softmax.
#define the loss functionloss=gluon.loss.SoftmaxCrossEntropyLoss()
O otimizador escolhido é descendência de gradiente estocástica, semelhante ao modelo anterior. Para este modelo, definimos tanto a taxa de aprendizagem como o impulso.
#Define the optimizertrainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':.02,'momentum':0.9})
Como você pode ver, mudamos alguns dos hiper-parâmetros: usamos o inicializador Xavier , adicionamos impulso ao otimizador, mudamos a taxa de aprendizado e adicionamos múltiplas camadas. A simplicidade de mudar estes e experimentar várias arquiteturas é uma das vantagens do uso do gluon .
Vamos agora treinar o modelo MLP.
#define variables/hyper-paramtersepochs=100moving_loss=0.best_accuracy=0.best_epoch=-1
#train the modelforeinrange ( epochs ): train_data . reset () for i , batch in enumerate ( train_data ): data = batch .
data [ 0 ] . as_in_context ( ctx ) label = batch . label [ 0 ] . as_in_context ( ctx ) with autograd .
record (): output = net ( data ) cross_entropy = loss ( output , label ) cross_entropy . trainer backward
() . step ( data . shape [ 0 ]) if i == 0 : moving_loss = nd . mean ( cross_entropy ) . asscalar () else :
moving_loss = . 99 * moving_loss . 01 * nd . mean ( cross_entropy ) . asscalar () _ , val_accuracy =
evaluate_accuracy ( val_data , net ) _ , train_accuracy = evaluate_accuracy ( train_data , net )
if val_accuracy > best_accuracy : best_accuracy = val_accuracy if best_epoch !=- 1 : print
( 'deleting previous checkpoint...' ) os . remove ( 'mlp- %d .params' % ( best_epoch )) best_epoch = e print
( 'Best validation accuracy found. Checkpointing...' ) net . save_params ( 'mlp-"si">% d .params' % ( e ))
print ( "Epoch %s . Loss: %s , Train_acc %s , Val_acc %s " % ( e , moving_loss , train_accuracy ,
val_accuracy ))
Best validation accuracy found. Checkpointing... Epoch 99. Loss: 0.021456909065, Train_acc 0.99498997996, Val_acc 0.44902
A precisão do treinamento parece ser boa, mas a precisão da validação é terrível. Uma possível causa é a sobreposição. Em uma configuração prática, teríamos arrastado os dados e os conjuntos de dados de trem, validação e teste teriam uma melhor parcela de bits mais altos e mais baixos.
Vamos agora prever o modelo no conjunto de dados de teste.
#Load the parametersnet.load_params('mlp-%d.params'%(best_epoch),ctx)
#predict on the test datasetpredictions,test_accuracy=evaluate_accuracy(test_data,net)output=np.vectorize(fizz_buzz)(np.arange(1,101),predictions.asnumpy().astype(np.int))(output)("Test Accuracy : ",test_accuracy)
['1' '2' '3' '4' 'buzz' '6' '7' '8' 'fizz' 'buzz' '11' 'fizz' '13' '14' '15' 'buzz' '17' 'fizz' '19' 'buzz' 'fizz' '22' '23' 'fizz' 'buzz' '26' 'fizz' '28' '29' 'fizzbuzz' '31' 'buzz' 'fizz' '34' 'buzz' 'fizz' '37' '38' '39' 'buzz' '41' 'fizz' '43' 'buzz' '45' 'buzz' '47' 'fizz' '49' 'buzz' 'fizz' '52' '53' 'fizz' 'buzz' '56' 'fizz' '58' '59' 'fizz' 'buzz' '62' 'fizz' '64' 'buzz' '66' '67' '68' '69' 'buzz' '71' 'fizz' '73' '74' '75' '76' '77' '78' '79' 'buzz' 'fizz' '82' '83' 'fizz' 'buzz' '86' '87' '88' '89' 'fizzbuzz' '91' '92' 'fizz' '94' 'buzz' 'fizz' '97' '98' '99' 'buzz'] Test Accuracy : 0.83
A precisão do teste é de 83%.
A adição de mais camadas ocultas levou a uma melhoria da precisão. É possível experimentar mais épocas e / ou mais camadas ocultas com diferentes funções de ativação para ver se a precisão melhora.
Conclusão e próximos passos
Este artigo forneceu uma rápida visão geral sobre como começar com o mxnet e o gluon . Com gluon , prototipagem e experimentação com várias arquiteturas é muito mais rápido. E o autograd permite-nos gravar o histórico de computação de forma a calcular gradientes mais tarde.
E vimos que o fizzbuzz é mais complexo do que parece, e fornece uma ótima base para o estudo de diferentes abordagens de aprendizado de máquina.
O droga reta tem um bom conjunto de tutoriais para começar com o mxnet .
Esta publicação faz parte de uma colaboração entre O‘Reilly e Amazon. Veja nossa declaração de independência editorial .
Contact Information:
Bargava Subramanian
Tags:
, Wire, Artificial Intelligence Newswire, United States, Portuguese
Keywords: afds, afdsafds










